F 分配

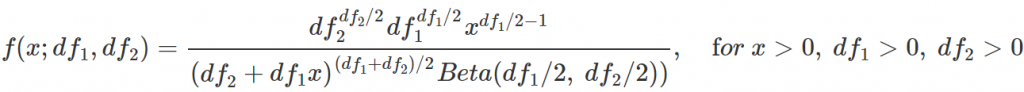
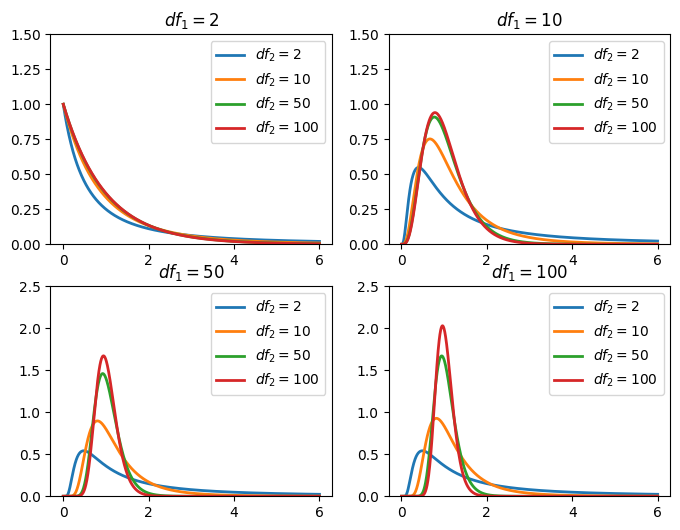
F 分配在 Python 的 PDF 程式代碼為 f.pdf ，其程式所使用的 PDF 如上，函數共具 2 個不同的參數 $df_1$ 與 $df_2$，函數的形狀由此些參數決定。如下圖，可以看出：

1. 當 $df_1 = 2$ 時，PDF 為右偏且凹口向上，隨著 $df_2$ 越小，曲線越下凹。
2. 當 $df_1 = 10$ 時，PDF 為右偏，隨著 $df_2$ 越大，曲線的最大值與平均數越大。
3. 當 $df_2$ 固定時，隨 $df_1$ 越大，曲線的峰度越大，且峰度的變化程度與$df_2$ 之大小有正向關係。

# F distribution

from scipy.stats import f

xlim_f = [0, 6]
x_diff_f = np.linspace(xlim_f[0], xlim_f[1], 10000)
color = np.array(['red', 'orange', 'yellow', 'green'])

# fig1

df1 = 2
df2 = np.array([2, 10, 50, 100])

fig, ax = plt.subplots(2, 2, figsize=[8, 6])
for i in df2:
  Y = f.pdf(x_diff_f, df1, i)
  ax[0][0].plot(x_diff_f, Y, linewidth=2, #color=color[i], \
                label=r'$df_2 = {}$'.format(i))
  
ax[0][0].legend()
ax[0][0].grid(False)
ax[0][0].set_ylim([0, 1.5])
ax[0][0].set_title(r'$df_1 = 2$')


# fig2

df1 = 10
df2 = np.array([2, 10, 50, 100])

for i in df2:
  Y = f.pdf(x_diff_f, df1, i)
  ax[0][1].plot(x_diff_f, Y, linewidth=2, #color=color[i], \
                label=r'$df_2 = {}$'.format(i))
  
ax[0][1].legend()
ax[0][1].grid(False)
ax[0][1].set_ylim([0, 1.5])
ax[0][1].set_title(r'$df_1 = 10$')


# fig3

df1 = 50
df2 = np.array([2, 10, 50, 100])

for i in df2:
  Y = f.pdf(x_diff_f, df1, i)
  ax[1][0].plot(x_diff_f, Y, linewidth=2, #color=color[i], \
                label=r'$df_2 = {}$'.format(i))
  
ax[1][0].legend()
ax[1][0].grid(False)
ax[1][0].set_ylim([0, 2.5])
ax[1][0].set_title(r'$df_1 = 50$')


# fig4

df1 = 100
df2 = np.array([2, 10, 50, 100])

for i in df2:
  Y = f.pdf(x_diff_f, df1, i)
  ax[1][1].plot(x_diff_f, Y, linewidth=2, #color=color[i], \
                label=r'$df_2 = {}$'.format(i))
  
ax[1][1].legend()
ax[1][1].grid(False)
ax[1][1].set_ylim([0, 2.5])
ax[1][1].set_title(r'$df_1 = 100$')

plt.show()

Normal

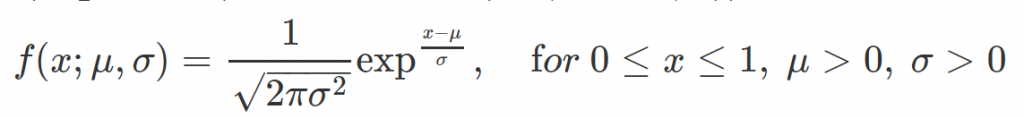
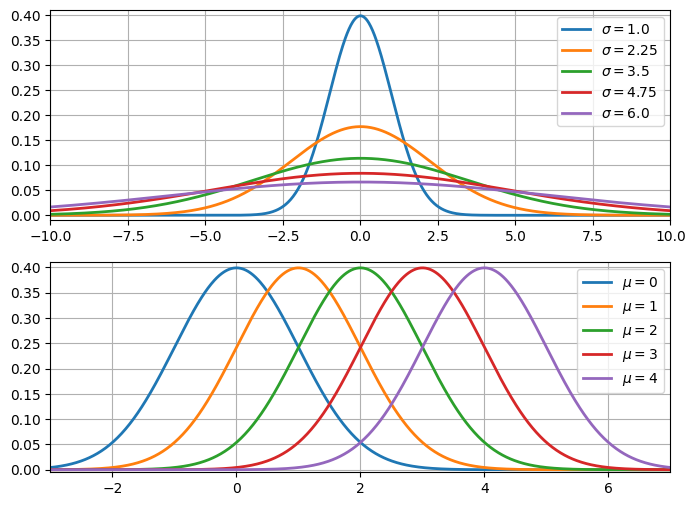
Normal 分配的 PDF 在 Python 中的程式碼為 norm.pdf ，其程式所依據的 PDF 如上式。設定不同的參數 $\mu$ 與 $\sigma$ 之下，如下圖，可觀察到隨 $\sigma$ 增大，PDF 越呈厚尾，其峰度也越小。而當 $\sigma$ 固定，隨 $\mu$ 變動，PDF 對稱的中軸線也隨之平移，但曲線的形狀（峰度與偏度）沒有改變。

# Normal distribution

from scipy.stats import norm


# sigma = np.linspace(1, 5+1, 1)
# mu = np.linspace(0, 4+1, 4)

fig, ax = plt.subplots(2, 1, figsize=[8, 6], squeeze=False)


# fig1 -- different sigma 
xlim = [-10., 10.]
x_diff_normal_scale = np.linspace(xlim[0], xlim[1], 1000)
mu = 0
sigma = np.linspace(1, 5+1, 5)


for i in sigma:
  Y = norm.pdf(x_diff_normal_scale, loc=mu, scale=i) 
  ax[0][0].plot(x_diff_normal_scale, Y, linewidth=2, \
                label=r'$\sigma = {}$'.format(i))
  

ax[0][0].set_xticks(np.arange(xlim[0], xlim[1]+2.5, 2.5))
ax[0][0].set_xlim(xlim)

ax[0][0].set_yticks(np.arange(0, 0.4+0.05, 0.05))
ax[0][0].set_ylim(0-0.01, 0.4+0.01)

ax[0][0].grid(True)
ax[0][0].legend()


# fig2 -- different mu
xlim = [-4., 9]
x_diff_normal_location = np.linspace(xlim[0], xlim[1], 1000)
mu = np.linspace(0, 4, 5, dtype=int)
sigma = 1


for i in mu:
  Y = norm.pdf(x_diff_normal_location, loc=i, scale=sigma) 
  ax[1][0].plot(x_diff_normal_location, Y, linewidth=2, \
                label=r'$\mu = {}$'.format(i))
  

ax[1][0].set_xticks(np.arange(xlim[0], xlim[1]+2, 2))
ax[1][0].set_xlim(-3, 7)

ax[1][0].set_yticks(np.arange(0, 0.4+0.05, 0.05))
ax[1][0].set_ylim(0-0.005, 0.4+0.01)

ax[1][0].grid(True)
ax[1][0].legend()

plt.show()

連續型的機率分配介紹到這裡結束，下篇開始介紹離散型分配，分配包含：Negative Binomial、Geometric、Hypergeometric。